ARIMA vs. long term forecasts

© 2017 Anton Lebedevich

Anton Lebedevich:

  • data science engineer
  • solves distributed performance issues
  • loves time series and anomalies
  • blogs at mabrek.github.io
A time series is a collection of observations made sequentially in time.

Forecasting Task (daily)

Forecasting Task (daily)

Forecasting Task (half-hourly)

Forecasting Challenges

  • multi-step ahead
  • many seasons (year, month?, week, day)
  • external predictors (weather, promo)
  • data gaps
  • outliers, changepoints
  • holidays (zero values)
  • irregular (sometimes)
  • short train

SARIMA

$$ \phi_p (L) \tilde \phi_P (L^s) \Delta^d \Delta_s^D y_t = A(t) + \theta_q (L) \tilde \theta_Q (L^s) \zeta_t $$

SARIMA

$$ \phi_p (L) \tilde \phi_P (L^s) \Delta^d \Delta_s^D y_t = A(t) + \theta_q (L) \tilde \theta_Q (L^s) \zeta_t $$

ARIMA (simple form)

$$ y'_{t} = c + \phi_{1}y'_{t-1} + \cdots + \phi_{p}y'_{t-p} \\ + \theta_{1}e_{t-1} + \cdots + \theta_{q}e_{t-q} + e_{t} $$

Dirac Delta Function

used to measure impulse response

AR(1) Impulse Response

$$ y_{t} = 0.9y_{t-1} + e_{t} $$

AR(2) Impulse Response

$$ y_{t} = 0.3y_{t-1} + 0.3y_{t-2} + e_{t} $$

AR(2) Impulse Response

$$ y_{t} = 0.9y_{t-1} - 0.85y_{t-2} + e_{t} $$

AR(2) Impulse Response

$$ y_{t} = 0.08y_{t-1} + 0.9y_{t-2} + e_{t} $$

I(0) Process (White Noise)

$$ y_{t} \sim \mathcal{N}(0,1) $$

I(1) Process (Random Walk)

$$ y_{t} = y_{t-1} + e_{t} $$

I(2) Process

Weekly Pattern + Noise

auto.arima

ellisp.github.io/blog/2015/09/30/autoarima-success-rates

ARIMA(7, 0, 0)

SARIMAX Challenges

  • ÷ multi-step ahead
  • - many seasons (year, month, week, day)
  • + external predictors (weather, promo)
  • - data gaps
  • - outliers, changepoints
  • - holidays (zero values)
  • - irregular (sometimes)
  • ÷ short train

What to Do Instead

  • start with naïve
  • linear
  • trees (XGBoost, etc..)
  • combine models
  • neural networks
  • bayesian
  • multiple output
  • …

Naïve Methods

  • just keep last value
  • mean or median
  • seasonal

Linear Models

  • lags
  • categorical seasons
  • Fourier seasons
  • window aggregates
  • holiday shoulders
  • promo actions
  • …

Ensemble Models

simple average

Neural Networks

  • entity embeddings
  • LSTM
  • more layers
  • …

Bayesian

  • BSTS
  • Facebook's Prophet
  • PyDLM, PyFlux, PyMC3, PyStan

Multiple Output

  • Direct
  • DirRec
  • MIMO
  • DIRMO
  • …

Out-of-sample Extrapolation

ellisp.github.io/blog/2016/12/10/extrapolation

NN doesn't Extrapolate Too

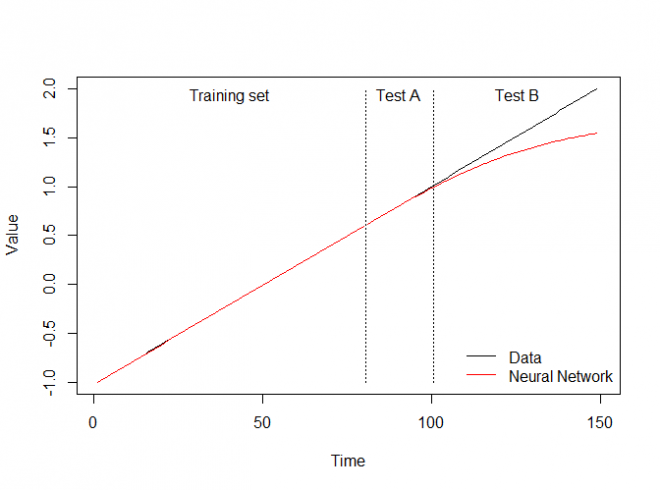
http://kourentzes.com/forecasting/2016/12/28/can-neural-networks-predict-trended-time-series/

Preprocessing for Trees and NN

Example Workflow

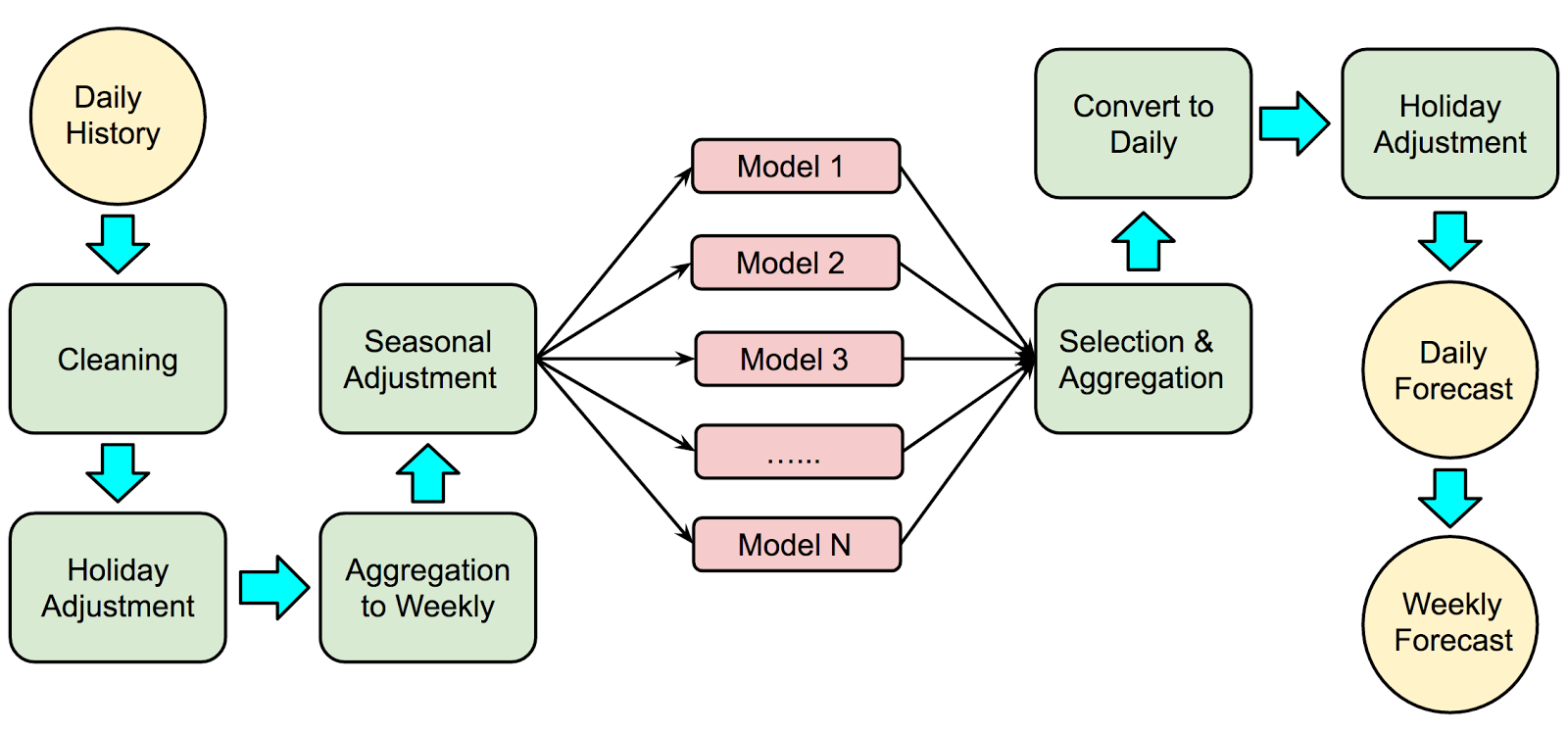www.unofficialgoogledatascience.com/2017/04/our-quest-for-robust-time-series.html

Competitions

Links

multithreaded.stitchfix.com/blog/2016/04/21/forget-arima/

robjhyndman.com/hyndsight/longseasonality/

www.unofficialgoogledatascience.com/2017/04/our-quest-for-robust-time-series.html

thuijskens.github.io/2016/08/03/time-series-forecasting/

video "Time-series and how to cook them with ML" by Alex Natekin @ Data Fest Kyiv 2017

github.com/robjhyndman/forecast

github.com/facebookincubator/prophet

forecasting textbook www.otexts.org/fpp

Q&A

Anton Lebedevich

mabrek@gmail.com

@widdoc

mabrek.github.io

mabrek.github.io/arima-vs-long-forecasts-2017