Introduces control charts based methods for production anomaly detection.
Let’s start with anomaly example which we’ve already seen in Data Properties:
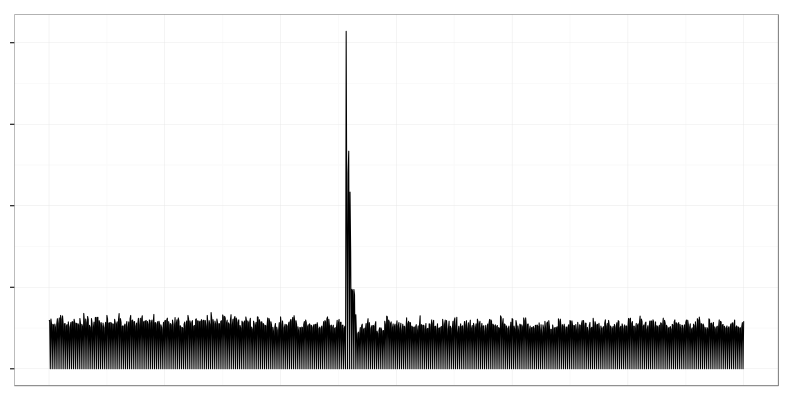
It’s a number of closed tcp sockets per second. One system crashed and a lot of clients got disconnected which resulted in large spike on the graph.
The graph has an interesting feature on zoomed in version:
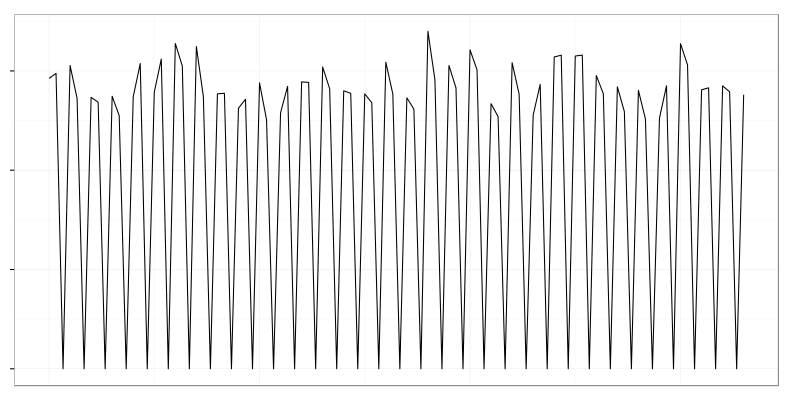
Counter was read faster than it was updated which lead to value 0 between every 2 normal values.
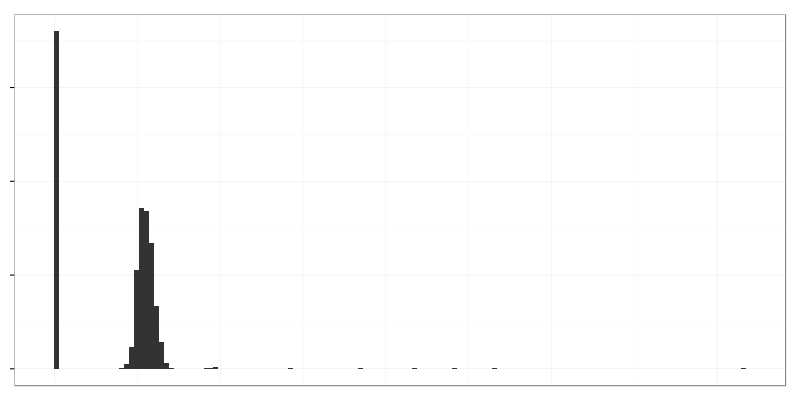
Histogram of the data shows large amount of zeroes (bar on the left), bell shaped distribution of ‘normal’ values (left middle), and anomalously large values from the spike (right side).
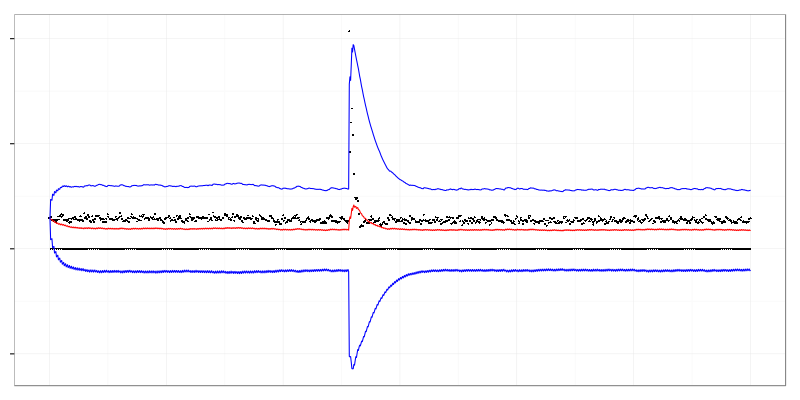
The simplest way to find that spike is to calculate moving average, moving standard deviation, and apply three-sigma rule. It’s also known as Shewhart control chart
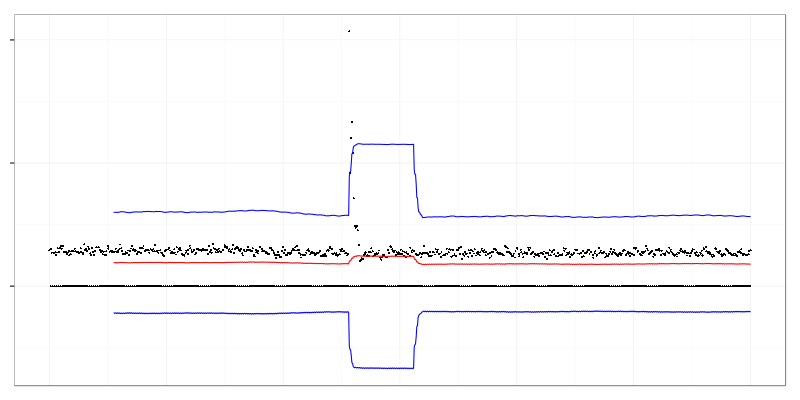
Black dots are data points, red is moving average, blue is three-sigma range around moving average. Values that fall off the range are considered anomalous.
There are several problems visible on the graph. It’s not possible to calculate ranges until there is enough data to fill calculation window. Bottom blue line is below 0 which doesn’t make sense because socket close frequency can’t go below 0. It’s caused by non-Gaussian distribution of data. Moving average and three-sigma range doesn’t return to normal values until spike leaves the window.
Exponentially-weighted moving average is based on the similar principle but it produces ranges from the beginning and recovers from anomalies faster:
These methods are good at finding outliers (spikes and drops) in data with distribution close to Gaussian or Poisson and flat trend (no growth or decline over time and no seasonal changes).